Last updated:
 Why Trust Cryptonews
Why Trust Cryptonews
Ad Disclosure
We believe in full transparency with our readers. Some of our content includes affiliate links, and we may earn a commission through these partnerships.

The Bank of England has released its latest research highlighting the potential of cutting-edge privacy technologies, such as zero-knowledge proofs (ZK-proofs), to bolster user privacy in a prospective digital pound.
The findings, outlined in the report titled “Enhancing the Privacy of a Digital Pound,” delve into how these technologies might safeguard user data while ensuring the functionality and security of a central bank digital currency (CBDC).
These innovations, which include pseudonymization, secure multiparty computing, and ZK-proofs, offer a way to minimize data sharing and give users greater control over their personal information.
ZK-Proofs: How Is The Bank of England Creating Its Digital Pound?
Zero-knowledge proofs, commonly called ZK-proofs, have garnered significant attention for their ability to verify information without revealing underlying data.
This cryptographic innovation has already seen widespread adoption in blockchain ecosystems like Ethereum, Zcash, and Polygon, where it enables privacy and scalability.
The Bank of England’s report suggests that integrating ZK-proofs into the digital pound could make it “at least as private as current forms of digital money, and potentially even more so.”
In addition to ZK-proofs, the research explores the potential of pseudonymization and secure multiparty computing.
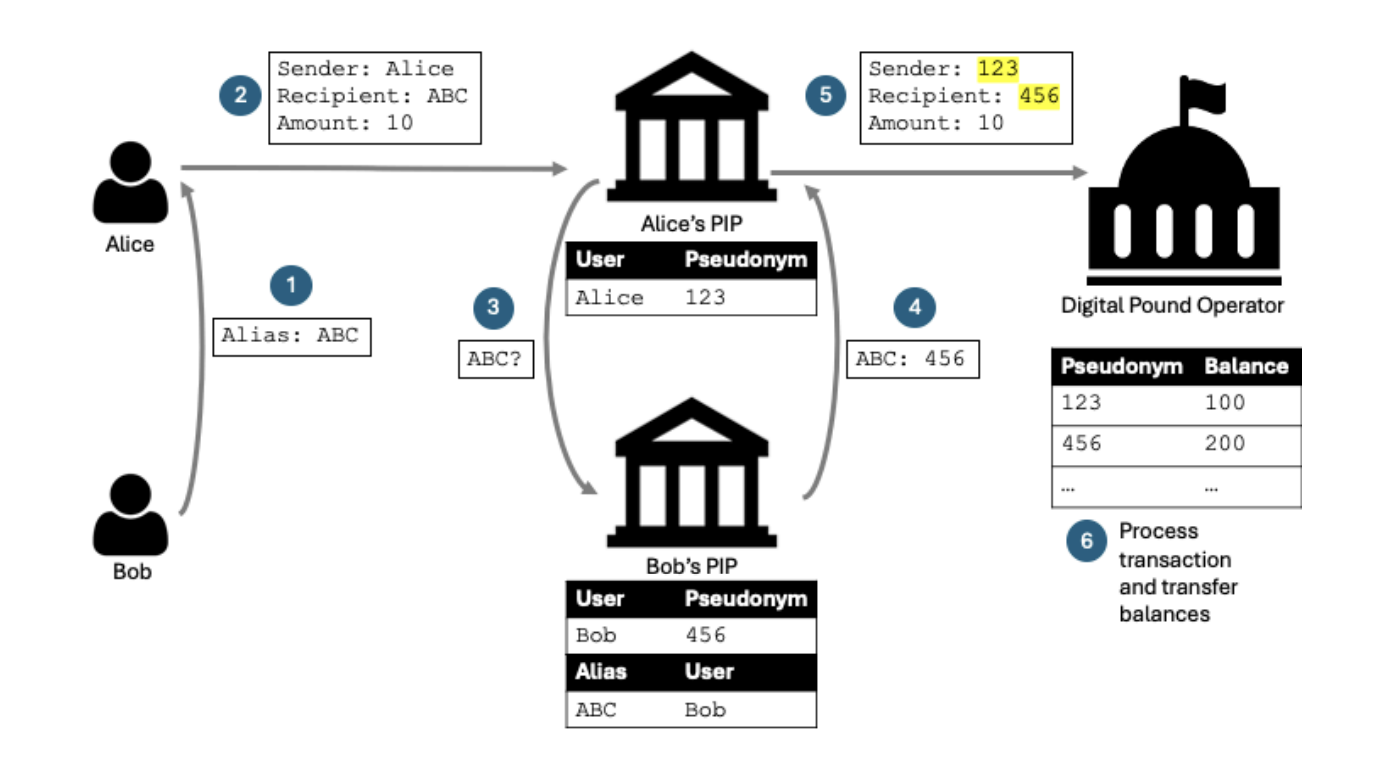
Pseudonymization could allow users to transact without exposing their full identity, meeting privacy needs while adhering to financial regulations.
Similarly, secure multiparty computing would enable transaction processing without any single entity accessing all transaction details, ensuring robust data protection and mitigating risks of unauthorized access.
The Bank of England has partnered with the Massachusetts Institute of Technology’s Digital Currency Initiative to assess the practical application of these technologies.
This collaboration aims to balance preserving user privacy and maintaining regulatory compliance. A challenge the report acknowledges as central to the CBDC’s design.
Privacy Challenges and the Path Forward
The Bank of England’s privacy-centric approach addresses the evolving digital payments landscape, where cash usage is waning and digital transactions are becoming the norm.
Through its 2023 public consultation, the bank identified privacy as a top concern among potential users. However, implementing privacy-enhancing technologies is not without challenges.
The bank’s report notes tensions between privacy measures and regulatory requirements that mandate data disclosure for anti-money laundering (AML) and counter-terrorism financing (CTF) purposes. This conflict necessitates further research to refine these technologies for real-world application.
Technical limitations also remain a hurdle, which was acknowledged in the report.
Despite these challenges, the bank is optimistic about these tools’ transformative potential in setting new standards for digital privacy.
Since establishing a task force in 2020 to explore a digital pound, the Bank of England has continuously emphasized the importance of adapting to technological advances.
The latest research marks another step in its ongoing evaluation and adoption consideration.
It is worth noting that no final decision has been made on launching a digital pound, but this research release signals a readiness to push it forward.
Notably, the Bank of England unveiled its plans earlier this year in July to experiment with distributed ledger technology (DLT) and wholesale central bank digital currencies (wCBDCs).
Through its participation in the earlier BIS Project Agora, the bank could test the tokenized asset exchange across multiple currencies on a unified platform.
The BoE’s approach involves synchronization with its Real Time Gross Settlement (RTGS) ledger and wCBDCs exclusively for financial institutions, aiming to enhance efficiency and programmability in monetary systems.





















